
That's what we learned in class today. Sorry it took so long to post this. I had a tennis match until seven and didn't get home until 7:30.
Jacob
P. S. The post time is wrong, I posted this around 8:45.

That's what we learned in class today. Sorry it took so long to post this. I had a tennis match until seven and didn't get home until 7:30.
Jacob
P. S. The post time is wrong, I posted this around 8:45.
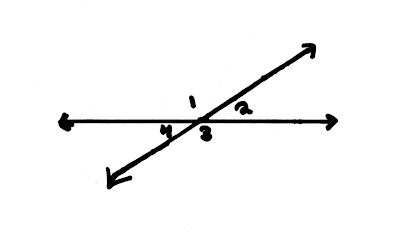
 1 and
1 and  2 are supplementary
2 are supplementary 2 and
2 and  3 are supplementary
3 are supplementary 3 and
3 and  4 are supplementary
4 are supplementary 4 and
4 and  1 are supplementary
1 are supplementary 1
1 
 3
3 2
2 
 4
4


 As you can see, these lines appear perpendicular. However, because there is no indication that they are, you can not assume anything!
As you can see, these lines appear perpendicular. However, because there is no indication that they are, you can not assume anything! This is the exact same picture as before, except now there is a square to indicate a right angle, meaning that these lines definitely are perpendicular!
This is the exact same picture as before, except now there is a square to indicate a right angle, meaning that these lines definitely are perpendicular!