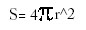Mr. Wilhelm-
Hi! I was just wondering when I should plan on taking the quiz. I heard that some people were taking it on Wednesday, before school. Thanks!
Jessica
Saturday, February 26, 2011
Wednesday, February 16, 2011
10.3
Hello, friends!
We've gone through the entire class for blogs, so logically it must be my duty to once again do the first blog post.
Today we learned a couple of things.
1) there are 3 types of arcs
a) semicircles- 180 degree arcs (requires 3 points to name and identify)
b) major arcs- greater than 180 degrees (requires 3 points to name and identify)
c) minor arcs- less than 180 degrees (requires 2 points to name and identify)
2) Congruent arcs on different circles implies that the circles are congruent.
a) to be congruent, both the angle measure and the length must be the same.

3) Congruent chords implies congruent arcs which implies congruent central angles which implies congruent chords. Basically, if you have a congruent Chord, you can prove the other two (central angles and arcs) congruent. If you have one you can prove the other two. They're biconditional.

Alright, gang. I'm off for Orlando. Be good for Mr. Wilhelm and do 10 nice things a day for the next couple days till break. It'll make you feel good.
Shane McPartlin.
P.S.

March 6th. Get pumped.
We've gone through the entire class for blogs, so logically it must be my duty to once again do the first blog post.
Today we learned a couple of things.
1) there are 3 types of arcs
a) semicircles- 180 degree arcs (requires 3 points to name and identify)
b) major arcs- greater than 180 degrees (requires 3 points to name and identify)
c) minor arcs- less than 180 degrees (requires 2 points to name and identify)
2) Congruent arcs on different circles implies that the circles are congruent.
a) to be congruent, both the angle measure and the length must be the same.
3) Congruent chords implies congruent arcs which implies congruent central angles which implies congruent chords. Basically, if you have a congruent Chord, you can prove the other two (central angles and arcs) congruent. If you have one you can prove the other two. They're biconditional.
Alright, gang. I'm off for Orlando. Be good for Mr. Wilhelm and do 10 nice things a day for the next couple days till break. It'll make you feel good.
Shane Mc
P.S.
March 6th. Get pumped.
Tuesday, February 15, 2011
Circles YAY!
Today we learned about circles. And just pointing out that i was the last to post both Trimesters so ha.
A Circle is the set of all points in a plane that are a given distance form a given point in the plane. The given point is the center of the circle, and the given distance is the radius.
A chord is a segment joining any two points of a circle. The diameter is the longest chord, and is twice the radius. A secant line goes through two points on the circle. A tangent lines intercepts a circle at exactly one point(the point of tangency)
This is an externally tangent circle. These circles
are internally tangent.

These are concentric circles.
There were many theorems that we learned, they were...
-If a radius is perpendicular to a chord, then it bisects the chord.
-If a radius of a circle bisects a chord that is not a diameter, then it is perpendicular to that chord.
-The perpendicular bisector of a chord passes through the center of the circle.
We also found that you can find the center of a circle, when you aren't given a complete circle by drawing chords. And then using those silly compasses.
In 10.2 we learned about congruent chords. We learned two theorems.
-If two chords of a circle are equidistant from the center, then they are congruent.
-If two chords of a circle are congruent, then they are equidistant form the center of the circle.
If AB≅ CD then GM≅EM
If GM≅EM then AB≅CD
Click Here for more information.
I bet you just all lost didn't you?
Happy blogging
-Jennifer Kendall.
Wednesday, February 9, 2011
12.5/12.6 Volumes of Pyramids, Cones, and Spheres
Today in class we learned about the formulas to solve for the volumes of pyramids, cones, and spheres. These formulas came from sections 12.5 and 12.6 in our book.
 In this diagram, we will say the radius is 6 so we can use the formula for the volume of a sphere to find its volume....V=4/3 πr^3...V=4/3(216π)...V=288π
In this diagram, we will say the radius is 6 so we can use the formula for the volume of a sphere to find its volume....V=4/3 πr^3...V=4/3(216π)...V=288π
Well, that's about all we learned today in class from 12.5/12.6. Hope it helped. And here's a video and a math problem that helps us learn how to count to 12, which I think is very important to today's lesson.
 *12 = http://www.youtube.com/watch?v=3nG1ckY7thw
*12 = http://www.youtube.com/watch?v=3nG1ckY7thw
12.5- Volumes of Pyramids and Cones
Pyramid....
The volume of a pyramid =1/3Bh...where B stands for the area of the base and h stands for height

So, in this picture, let's say the height =8 and the area of the base is 48. To solve for the volume, you use the formula....V=1/3Bh....V=1/3(48)(8).....V=1/3(384)....so V=128
Cones
The formula to find the area of a cone = 1/3Bh which in this case =1/3πr^2h where r stands for radius length and h stnds for height.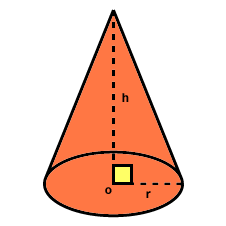
In this picture of a cone, let's say the height is 7 and the radius is 3. With this information we can find the volume of the cone using the formula..... V=1/3πr^2h....V= 1/3(9π)(7)...V=1/3(63π)...V=21π
12.6
Volumes of Spheres
The volume of a sphere =4/3 πr^3 where r is the radius.
 In this diagram, we will say the radius is 6 so we can use the formula for the volume of a sphere to find its volume....V=4/3 πr^3...V=4/3(216π)...V=288π
In this diagram, we will say the radius is 6 so we can use the formula for the volume of a sphere to find its volume....V=4/3 πr^3...V=4/3(216π)...V=288πWell, that's about all we learned today in class from 12.5/12.6. Hope it helped. And here's a video and a math problem that helps us learn how to count to 12, which I think is very important to today's lesson.
 *12 = http://www.youtube.com/watch?v=3nG1ckY7thw
*12 = http://www.youtube.com/watch?v=3nG1ckY7thwThanks, Michael
2/9/11
Tuesday, February 8, 2011
12.4 Volume of Prisms and Cylinders
Hello fellow classmates, and teachers,
If you are unaware, or you were absent, or you didn't read the title, today we learned about volume. Below you will locate a written description and example sheet of volume and a video link. You may choose whichever suits you best. Mr Wilhelm, as you are aware I'm not here in first hour today. Knowing this would you be kind enough to show my classmates the hidden hint and puzzle for them to solve? If you would that would be very sincere, if not, well then I understand. Thanks, and Enjoy.
HINT: CONGRATS!!! After I tried so hard to hide this hint you still managed to process its whereabouts!!! If you would like to "LOSE THE GAME" then you must both read the blog and watch the video. Good Luck!
Volume: measures capacity
Volume: the amount of cubic units taken to fill a 3 dimensional figure
Sorry for any inconvenience, the "blach" was a B, I think the mic on my phone stalled out,
and the vibration noise was my phone ringing. It was the best take I had.
The equation for volume is represented by V=B(h)
With "V" representing volume, "B" representing the total area of the base of the figure, and "h" representing its height.
For example, the formula of a triangular prism: V= [1/2(bh)]H
rectangular prism: V=lwh
Cylinder: V=πr²(H)
and so on...


Blog of the year?
Thank you for reading thy blog post, please subscribe,
I hope you enjoyed everything, for there is a possibility
that this may be my last blog post, (last trimester with Mr. Wilhelm)
Sincerely, Your loyal blogger, cough cough (Peter Kessel),
Oran Lieberman
P.S, the purple letters spell out, I LOST THE GAME.
Labels:
10th grade,
12.4,
cylinder,
cylinders,
Fun,
geometry,
honors geometry,
math,
prism,
prisms,
volume
Monday, February 7, 2011
Areas of Cones and Others
 Okay so heres the problem we did in class in case you dont have it. We needed to fine the surface area for it. The formula for surface area is:
Okay so heres the problem we did in class in case you dont have it. We needed to fine the surface area for it. The formula for surface area is:S= 2B + ph
All you have to do is take the numbers you already have and plug them into the formula.
Then....
Cylinders:
If you want to find the surface area of a cylinder, you use the formula that has been circled in yellow. It tells you what is needed to find the base and perimeter.
And...
Spheres:
The formula to find the surface area of a sphere is:
And when you want the formula for a hemisphere, its easy to figure out. You cut the circle in half. Then, since you cut it, you added another circle (like a face) to it. It looks like,
So, since you have half the cirlce, you divide the original formula in half. But, you have to add that new "face" in, so add one more area of a circle to that. You end up with,
And lastly...
Cones:
Theres also the Frustum of a cone. It looks like....
To find its surface area really isnt that difficult. All it is isWhen the letters are big, it means from the big circle, and when they are small, it means the little circle.
I think thats about it, sorry if some pictures are a little confusing.
And just for fun, i lost the game :]
Kristy
Friday, February 4, 2011
Surface Area of Prisms and Pyramids
Hey class it's eLeni (5th last person to get the blog post)
Friday we learned how to find surface area of prisms, pyramids, and other irregular shapes that "make this honors geometry" as well as develop some formulas.
Mr.W starts with the example of a tissue box, which is a rectangle prism.
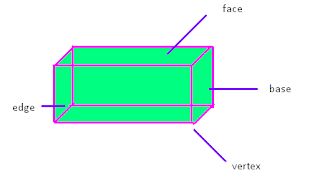
We review what faces, edges, and vertices are (in diagram).
We define Surface Area as the area of a surface. (Thank you, Shane)
Also, Polygon as a closed, straight-sided figure
Polyhedrons are 3D figures with straight sides, faces, and is also a closed figure
The Polyhedron shapes we will be learning about are Prisms and Pyramids
and the circular shapes are cylinders, cones, and spheres
Prisms are polyhedrons with two congruent faces that are connected by rectangles
Next, we learned Base which are the two parallel congruent faces (also in picture)
Lateral Faces are the faces that are not bases (In our rectangular prism example, they are rectangles)
Anti prisms Prisms in which the lateral faces are triangles
Friday we learned how to find surface area of prisms, pyramids, and other irregular shapes that "make this honors geometry" as well as develop some formulas.
Mr.W starts with the example of a tissue box, which is a rectangle prism.
We review what faces, edges, and vertices are (in diagram).
We define Surface Area as the area of a surface. (Thank you, Shane)
Also, Polygon as a closed, straight-sided figure
Polyhedrons are 3D figures with straight sides, faces, and is also a closed figure
The Polyhedron shapes we will be learning about are Prisms and Pyramids
and the circular shapes are cylinders, cones, and spheres
Prisms are polyhedrons with two congruent faces that are connected by rectangles
Next, we learned Base which are the two parallel congruent faces (also in picture)
Lateral Faces are the faces that are not bases (In our rectangular prism example, they are rectangles)
Anti prisms Prisms in which the lateral faces are triangles
Euler's Formula
This is pronounced "Oiler" (just so you don't sound like a fool in Mr. B's class)
To understand his formula, we made a chart of things we knew until we found some nice patterns.
Rectangular Prism Square Pyramid Triangular Prism Triangular Pyramid
F (Faces) 6 5 5 4
V (vertices) 8 5 6 4
E (Edges) 12 8 9 6
We could then find these short formula/ideas
Rectangular Prism Square Pyramid Triangular Prism Triangular Pyramid
F (Faces) 6 5 5 4
V (vertices) 8 5 6 4
E (Edges) 12 8 9 6
We could then find these short formula/ideas
N-gonal Prism N-gonal Pyramid
F (Faces) n+2 n+1
V (vertices) 2n n+1
E (Edges) 3n 2n
I guess these are all just nifty things to know. Euler's Formula is F+V=E+2 (Variables same as chart)
Net-3D shapes are unfolded
This is a net of a Cube (A six-faces 3D shape of congruent squares)
Check out the net of a Cylinder:
It's really just a rectangle and two circles (faces)
F (Faces) n+2 n+1
V (vertices) 2n n+1
E (Edges) 3n 2n
I guess these are all just nifty things to know. Euler's Formula is F+V=E+2 (Variables same as chart)
Net-3D shapes are unfolded
This is a net of a Cube (A six-faces 3D shape of congruent squares)
Check out the net of a Cylinder:
It's really just a rectangle and two circles (faces)
This is the net of a cone.
*Notice that that is a circle and a sector
You can see that the L (Lateral Area) can be further broken up so that L= n (1/2 bh). This is the number of lateral faces which are triangle that have the area 1/2bh. This formula is then simplified again to be L=n (1/2 s) (l). l=slant height.
*Make sure the slant height is perpendicular to the base
*Notice that that is a circle and a sector
SURFACE AREA
1. Prism: S=2B+ph
S=Surface Area, B=Area of base, p= perimeter of base, h=height
2. L=ph
L=Lateral Area, P=perimeter of base, h=height
3. Pyramid: S= B+L
#3 is the most basic form of the formula, but can be altered to be more useful
You can see that the L (Lateral Area) can be further broken up so that L= n (1/2 bh). This is the number of lateral faces which are triangle that have the area 1/2bh. This formula is then simplified again to be L=n (1/2 s) (l). l=slant height.
*Make sure the slant height is perpendicular to the base
HONORS GEOMETRY FUN
The surface area for this interesting thing would be
S=L(prism)+B(prism)+L(pyramid)
which can be simplified to S= ph+B+ 1/2 pl
*Remember that if you're finding them separately, the SA is not the SA of the pyramid+prism. This is because they share a common face
In this figure, a prism with square bases has been cut out of a rectangular prism.
Thus, S=L(big prism)+2B(big)-2B(small)+L
Or S=L(b)+L(s)+2(Bb+Bs)
This S happens to equal (2x+2y)z+(4a)z+2(xy+a^2)
I also found out where Mr.W got his cool 3D shapes!!!!
Adios, eLeni
Subscribe to:
Posts (Atom)