Surface Area of Prisms and Pyramids

Hey class it's eLeni (5th last person to get the blog post)
Friday we learned how to find surface area of prisms, pyramids, and other irregular shapes that "make this honors geometry" as well as develop some formulas.

Mr.W starts with the example of a tissue box, which is a rectangle prism.
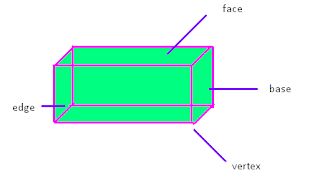
We review what faces, edges, and vertices are (in diagram).

We define Surface Area as the area of a surface. (Thank you, Shane)
Also, Polygon as a closed, straight-sided figure 
Polyhedrons are 3D figures with straight sides, faces, and is also a closed figure 
The Polyhedron shapes we will be learning about are Prisms and Pyramids
and the circular shapes are cylinders, cones, and spheres
Prisms  are polyhedrons with two congruent faces that are connected by rectangles
 Next, we learned Base which are the two parallel congruent faces (also in picture)
Lateral Faces  are the faces that are not bases (In our rectangular prism example, they are rectangles) 
Anti prisms  Prisms in which the lateral faces are triangles

Euler's Formula

This is pronounced "Oiler" (just so you don't sound like a fool in Mr. B's class)

To understand his formula, we made a chart of things we knew until we found some nice patterns.
  Rectangular Prism    Square Pyramid    Triangular Prism    Triangular Pyramid
F (Faces)           6                                5                        5                              4
V (vertices)        8                                5                        6                              4
E (Edges)          12                               8                        9                              6
We could then find these short formula/ideas

                  N-gonal Prism    N-gonal Pyramid
F (Faces)          n+2                     n+1
V (vertices)       2n                       n+1
E (Edges)          3n                        2n
I guess these are all just nifty things to know. Euler's Formula is F+V=E+2 (Variables same as chart)

Net-3D shapes are unfolded

This is a net of a Cube (A six-faces 3D shape of congruent squares)
Check out the net of a Cylinder:

It's really just a rectangle and two circles (faces)

This is the net of a cone.

*Notice that that is a circle and a sector

SURFACE AREA

1. Prism: S=2B+ph

          S=Surface Area, B=Area of base, p= perimeter of base, h=height

2. L=ph

           L=Lateral Area, P=perimeter of base, h=height

3. Pyramid: S= B+L 

         #3 is the most basic form of the formula, but can  be altered to be more useful

You can see that the L (Lateral Area) can be further broken up so that L= n (1/2 bh). This is the number of lateral faces which are triangle that have the area 1/2bh.  This formula is then simplified again to be  L=n (1/2 s) (l). l=slant height.
*Make sure the slant height is perpendicular to the base

 

HONORS GEOMETRY FUN

 The surface area for this interesting thing would be 

S=L(prism)+B(prism)+L(pyramid)

which can be simplified to S= ph+B+ 1/2 pl

*Remember that if you're finding them separately, the SA is not the SA of the pyramid+prism. This is because they share a common face

In this figure, a prism with square bases has been cut out of a rectangular prism.

Thus, S=L(big prism)+2B(big)-2B(small)+L

Or S=L(b)+L(s)+2(Bb+Bs)

This S happens to equal (2x+2y)z+(4a)z+2(xy+a^2)

I also found out where Mr.W got his cool 3D shapes!!!!

 

Adios, eLeni