Anyways today we learned about the pythagorean theorem and how there are many ways to prove it...
Here are the three ways we learned in class
The first way is...................
Start with a triangle
The area of one such triangle is of course 1/2ab (1/2Base x Height)
The area of four triangles identical to the original is 2ab (1/2ab x 4)
Now imagine it like this
The area of the large square is

The area of the small square is

so

That simplifies to
 or the pythagorean theorem
or the pythagorean theoremThe next way to prove it is to start with another triangle

Now picture this
The area of the large square is

And the area of the smaller square is

So you can set up the equation

Which again makes

*BONUS PROOF*
area of the green square is
area of the blue square is
area of the red square is
OR
I lost the game :(
(Shane this is where you yell "I lost the game!")
David Mahoney




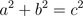
No comments:
Post a Comment