Law of SINES/COSINES

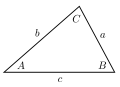
Fellow Classmates, Mr. Wilhelm, and Stalkers I Don't Know, Friday we learned A. the best way to make your math teacher happy is to hide all of their stuff B. that #A does not apply to Mr. Wilhelm C. #A is actually a letter D. stuff about shapes . . This beautifully color-coded picture illustrates an oblique trigon. Oblique trigons are sad because everyone groans when they see them because their measurements don't do any thing special. "Oh how I wish I could be a SPECIAL triangle!" said a young triangle. One day, Mr. Wilhelm invented a formula for them called THE LAW OF SINES . You plug in an angle (A), the side opposite it (a), and one other piece of information (angle C or side c). You can then solve for the other piece's counterpart (side c or angle C). You (and the triangles) can consider it something of a hero. . . This formula happens to be THE LAW OF SINES don't crowd it . . This is the same triangle from before. Cheap Budget. . . These formulas make up the LAW OF COSINES. The formulas on the left work when you are given SAS. The formulas on the right work when you are given SSS. . . . Here is a website that proves the law of sines Here is a website that proves the law of cosines Here is a website that exemplifies stuff Watch the video about sines and cosines It dosen't work.. but it shows the importance of apologies and good pouty faces Here is an unrelated website . . 'sine' ing off ~~OLIVIA MILLER~~

11.8 Hero's and Brahmagupta's Formulas

Section 11.8 was about Hero's and Brahmagupta's Formulas. Also, we learned an equation for the area of a triangle when SAS is given. 

SAS

Hero's Formula-(for area of triangles)

                                                  
                     

where a, b, and c are the side lengths









Brahmagupta's Formula-(for CYCLIC quadrilaterals ONLY)

where a, b, c, and d are the side lengths

Well, Hero and Brahmagupta were math geniuses, but they will never be able to top the great Mr. Wilhelm.

God Bless Blog Posts

(and the game)

Joey

11.7

Hey guys. This was an easy section. Yeah.

One was of determining the ratio of the areas of two figures is to calculate the quotient of the two areas.

As in, lets say a triangle has a height of 8 and a base of 12. And yes, I'm way too lazy to actually find a picture or draw one that corresponds to this. And theres another figure, a parallelogram with a height of 9 and a base of 12.

Everyone here should know the formulas for these areas, but in case you needed to be reminded:
A of Triangle= 1/2BH, where B=Base and H=Height
A of Parallelogram= BH, where B=Base and H=Height

So, if you wanted to compare area of the Parallelogram to the area of the triangle, you would first find the area of the parallelogram and then divide it by the area of the triangle.

A of Triangle= 1/2(8X12)=48
A of Parallelogram= 10X9= 90
which would be 90 over 48, and that simplifies to 15 over 8, or 15:8

One theorem we discussed in class is theorem 109, which states:
If two figures are similar, then the ratio of their areas equals the square of the ratio of corresponding segments. (Similar-Figures Theorem)

In other words, its basically this:

A1/A2=(S1/S2) squared.
where A1 and A2 are areas and S1 and S2 are measures of corresponding segments.

Another theorem we learned in the bum rush that is the end of class is Theorem 110, which states:
A median of a triangle divides the triangle into two triangles with equal areas.

In other words, Imagine a triangle PQS, nothing special about it.
Then, imagine a line from vertice P to seg. QS. The line bisects the segment at point R.
This theorem states that the Area of triangle PQR is = to the Area of triangle PRS

Imagination is better than knowledge. Or pictures. Or something.

http://artists.letssingit.com/daft-punk-lyrics-digital-love-6xcgscc
Last two lines are the best lyrics ever, by the way.

Chapter 11.6

Areas of Circles, Sectors, and Segments.


So friday in class we learned about sectors, segments, and ares of circles.

The area of a circle:
A sector of a circle is a regioun bounded by the two radii and an arc of the circle.

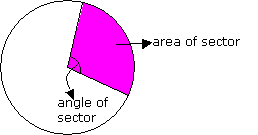Area of sector: A=(m/360)πr²

*where m=measure of arc

OR

http://www.mathopenref.com/arcsector.html

A segment of a circle of a circle is a region bounded by a chord of the circle and its corresponding arc.  

The yellow part above is the segment of the circle.

AB is the chord.

To find the segment of a circle= area of the sector-area of triangle AOB. That is the easiest way. In fomula way, A=(m/360)πr² -(1/2)bh

Where m=measure of arc AB and bh is base times height.

http://www.mathopenref.com/segmentarea.html

That's all we learned on Friday, pretty easy. Sorry it's posted so late!

-Elizabeth (lost the game) Quigley

Section 11.6

Today in class, we learned about finding the area of regular polygons, as well as the different parts. We know that all regular polygons can be inscribed in a circle.

In the hexagon, there are some important things that you should know.

• Segments OA and OB are radii of the circle and the polygon (yes, regular polygons have radii)
  
• Segment OG is an apothem, a segment joining the center to the midpoint of any side, and forms a right angle, so OG⊥AB.
  

The octagon shows you other parts of a regular polygon.

• Center- the center of a regular polygon


• Central angle- the angle formed at the center of the polygon by two segments from adjacent vertices.
  

To sum things up, here are some important things about apothems and radii:

• all apothems of a regular polygon are congruent
  
• only regular polygons have apothems


• an apothem is a perpendicular bisector of a side


• a radius of a regular polygon is a radius of a circle circumscribed about the polygon


• a radius of a regular polygon bisects an angle of the polygon.
  

Now on to the symbols of the parts of the polygon and the formula for the area. Also, uppercase and lowercase letters mean different things.

• A- area of the polygon


• p- perimiter of a polygon


• n- number of sides in a polygon


• s- length of a side of a polygon


• r- length of a radius of a polygon


• a- length of the apothem


• θ (theta)- measure of the central angle
  

The formula for the area of a regular polygon is 1/2 ap, or one half of the apothem times the perimeter. Also, 1/2 ans can be used for the area, as the number of sides in a polygon (n) times the side length (s) equals the perimeter (p).

That's all for this section, I hope our blog is popular at the conference tomorrow!

-Jacob

P. S. I lost the game.

11.3 & 11.4

Today in class we covered two sections: 11.3 and 11.4.

11.3 was about the area of a trapezoid. To find the area of the trapezoid, use this formula (in this formula, the a and b stand for the base 1 and base 2):





We learned that the formula comes from a few places, such as the ones shown below:

 
You can move the triangles on the sides up to the top of the trapezoid to create a rectangle. 

Here, it shows how the trapezoid the area formula is made. 

• The area of the rectangle is b₁h.
• The area of the triangle on the left side is ½xh.
• The area of the triangle on the right side
  is ½(b₂ – b₁ – x) × h = ½b₂h – ½b₁h – ½xh.
• The combined area of the three pieces, then,
  is b₁h + ½xh + ½b₂h – ½b₁h – ½xh, which simplifies to ½b₁h + ½b₂h. This further simplifies to ½(b₁ + b₂) h, which is the trapezoid area formula. 

(All of this info I found at http://illuminations.nctm.org/LessonDetail.aspx?ID=L580)

Another very helpful website is http://www.mathopenref.com/trapezoidarea.html

On it, you can change the base and the height in an interactive trapezoid. It also clearly explains the formula and has videos you can watch.

Next, we went on to 11.4, which was the area of kites and/or rhombi.
To the area of a kite or a rhombus, you use the formula A= ½ d₁d₂ 
This formula comes from the fact that a rectangle can be drawn around a kite or rhombus and that the kite or the rhombus can be "cut up" and then turned into a rectangle that has an area one half of the big rectangle.

That's about it! I hope that everyone loves our blog at the conference thing. Also, LOST THE GAME :)


-Jessica 

11.1 and 11.2

Today in class we learned about the area of two dimensional shapes

Area: the number of square units of space within the boundary of a region

Here's a few formula's for area:

rectangle: A=bh

parallelogram: A=bh

area of a rectangle=area of a parallelogram

triangle: A=(1/2)bh

circle:


We also learned a little about these postulates:



-If two closed figures are congruent, then their areas are equal



-If two closed regions intersect along a common boundary, then the area of their union is equal to the sum of their individual areas

the area of the whole shape=the area of the square + the area of the triangle

And thats basically it!
-Olivia

9.10

9.10 TRIGONOMETRIC RATIOS

SHANE

If you were looking from point (H) at the top of a flag pole (A), the angle the line of sight HA make with horizontal HM is called angle of elevation.

http://www.icoachmath.com/SiteMap/AngleofElevation.html

Humpy Dumpy sat on a wall at point F, looking down at a unicorn U, the angle of his line of sight FU with the horizontal FR is called the angle of depression.

http://www.icoachmath.com/SiteMap/Angleofdepression.html

http://www.youtube.com/watch?v=oLsZB1VzxQo

Sorry its small but this section is about a half a page.

once again,

Peter Kessel

9.9

9.9 INTRO TO TRIGONOMETRY
(this guys name is trigon)

nonagon, octagon, hexagon, pentagon, TRIGON

SOH CAH TOA

sine- (opposite leg/hypotenuse)

cosine- (adjacent/hypotenuse)

tangent- (opposite leg/adjacent leg)

http://www.youtube.com/watch?v=_S35Ht4imhs&feature=related and http://www.youtube.com/watch?v=XFh_JC7OSrg but because she is boring play this in the background http://www.youtube.com/watch?v=zPUiSfGNmAI

pETER kESSEL

9.8

On Friday, we learned about The Pythagorean Theorem and Space Figures.

We mostly deal with the rectangular solid and regular square pyramid.

Rectangular Solid:

CDHG is one of the 6 faces.

is one of the 12 edges.

is one of the 4 diagonals of the rectangular solid.

If you were give the dimensions 8, 9, and 12 in order to find the diaganol

, it wouldn't matter which edges you assigned the lengths to. So you could let EG=9, GH=12, and AE=8. Then use the pythagorean theorem to find EH=15. Now from using AE=8 and EH=15, you can use the pythagorean theorem to solve for AH which equals 17.

Regular Square Pyramid:

The base is a square.

The altitude is perpendicular to the base at its "center."

The slant height is perpendicular to the "side" of the base. To solve for the slant height, you would use pythagorean theorem with the height and half of the base.

Sorry this blog post was really short, but this section was short, so this pretty much covers it all.

-Megan

Sections 9.6 & 9.7

Hello everyone!
Today we covered two sections, 9.6 & 9.7
Lets start with 9.6
9.6 was a pretty short, simple section about families of right triangles and Pythagorean Triples.
A Pythagorean Triple is any three whole numbers that satisfy the Pythagorean theorem,
For example, 3,4,and 5 are Pythagorean triples. Also, 8, 15, and 17

Any multiples of these are also in the same family of right triangles. For example 6, 8, and 10. These are all multiples of 3,4,and 5, therefore they are in the same family.



Next, is section 9.7

Section 9.7 has some shortcuts when dealing with "special" right triangles.

The first trick is for dealing with right triangles that have angle measures of 30°, 60°, and 90°.

Let a represent the side length of the short leg of the triangle. The hypotenuse is 2a. The long leg is a

For example, in the picture to the left, if a=4, the hypotenuse=8, and the long leg=4.

If you are slightly confused, I found that drawing an equilateral triangle and then drawing an altitude showed the relationships more clearly. The video below shows how to do this.

The video was giving me a little trouble so if it doesn't work here's the link

http://www.youtube.com/watch?v=_eBIuP9pugM

The next shortcut is for isosceles right triangles. These triangles have angle measures of 45°, 45°, and 90°. Let a represent the side length of the leg. Because it's isosceles the other leg is also a. The hypotenuse however, is a.

That wraps up sections 9.6 and 9.7. They were short and relatively easy sections. Personally I would prefer if our math homework looked like this

If only,

Ryan