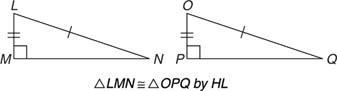
Terms

In order to understand the section, we must first understand the plane. A plane is a surface such that if any two points on the surface are connected by a line, all points of the line are also on the surface.

If points, lines, segments, and so forth lie in the same plane, they are coplanar. In the same way, if any of these do not lie in the same plane, they are noncoplanar.

Another term we need to be familiar with is transversal. A transversal is a line that intersects two coplanar lines in two distinct points.

In the diagram below, line n is the transversal. The region above line t and below line m is the exterior of the figure. The region between lines A and B is the interior of the figure.

Lines and Transversals create angle pairs. These angle pairs include: Corresponding Angles, Alternate Interior Angles, and Alternate Exterior Angles.

·         Corresponding Angles are a pair of angles formed by two lines and a transversal. One angle must lie in the interior of the figure and the other must lie in the exterior. The angles must lie on the same side of the transversal but have different vertices. Angle 1 and Angle 5 in the diagram above are examples of corresponding angles.

·         Alternate Interior Angles are a pair of angles formed by two lines and a transversal. Both angles must lie in the interior of the figure, must lie on alternate sides of the transversal and have different vertices. Angle 4 and Angle 6 in the diagram above are examples of alternate interior angles.

·         Alternate Exterior Angles are a pair of angles formed by two lines and a transversal. Both angles must lie in the exterior of the figure, must lie on alternate sides of the transversal, and have different vertices. Angle 2 and Angle 8 in the diagram above are an example of alternate exterior angles.

That should get us started on transversals and angle pairs,

thank you,

Ryan

Perpendicular Bisectors & Taxicab Geometry

Perpendicular Bisectors:

There are 2 new theorems for perpendicular bisectors that we learned today in class.

Theorem #1: 2 points equidistant to end points implies perpendicular bisector

An example of this theorem is shown here...

The word equidistant is defined as... The vertex is the same distance away from the 2 endpoints

The 2nd theorem we learned today was...

Theorem 2: A point on a perpendicular bisector implies equidistance from the 2 endpoints

Taxicab Geometry:

Taxicab Geometry can be defined as...a form of geometry in which the usual metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their coordinates

An example of taxicab geometry is shown here by a taxicab circle:

A taxicab circle is a circle in which all of the surrounding points are equal distance away from the center of the circle, and take the shortest route to that given point.

That's just about all we learned in class today. Thank you.

-Michael Levitsky

HL Postulate

HL Postulate

If the hypotenuse and leg of one right triangle are congruent to the corresponding parts of another right triangle, then the triangles are congruent (Figure 6 ). 

Figure 6 The hypotenuse and one leg (HL) of the first right triangle are congruent to the corresponding parts of the second right triangle.

It is important that the HL Postulate ONLY applies to RIGHT triangles. So when using in a proof, one statement must be that the triangles are right triangles.


Thanks to everyone for their support in getting me to do the blog.
Joey

Types of Triangles

SCALENE TRIANGLE- NO SIDES ARE CONGRUENT

EQUILATERAL TRIANGLE-ALL THREE SIDES CONGRUENT

 

 

EQUILATERAL IF AND ONLY IF EQUIANGULAR

ISOSCELES TRIANGLE-

• AT LEAST TWO SIDES CONGRUENT
• THE TWO CONGRUENT SIDES ARE CALLED THE LEGS
• THE NON-CONGRUENT SIDE IS CALLED THE BASE
• (AN EQUILATERAL TRIANGLE IS STILL AN ISOSCELES TRIANGLE)

YOU'RE WELCOME

3.4: Beyond CPCTC

Today in class, we learned about 4 new terms about triangles and their proofs.

These terms are Perpendicular Bisector, Angle Bisector, Altitude, and Median


Perpendicular Bisector- a straight line that is perpendicular to a segment at its midpoint

Angle Bisector- a straight line that divides an angle into 2 equal parts

Altitude- a straight line through a vertex of the triangle and perpendicular to the oppposite side

Median- a straight line from a vertex of a triangle to the midpoint of the oppsite side

Ok thats pretty much everything we learned about in class today. In section 3.4, we will be doing the same thing as 3.3 but going a bit further by using the statement that two triangles are congruent. A few of these terms will also show up in the homework.

Thanks,

Robbie

3.3 CPCTC and Circles

Today in class we learned about circles and CPCTC, or Corresponding Parts of Congruent Triangles are Congruent. 

First of all, we defined what a circle is. A circle is a set of points that are equidistant from a given point. Also, the circle is just the circumference, or the outside border, and the inside is called the "disk", as shown below:

Secondly, every circle is named by its center point. Again, the circle consists of only the "rim", as the book refers to it, so the center point is not part of the circle. To show the name of the circle, you would draw a small circle with a dot in the middle and then write the letter of the center. (Sorry I couldn't find a good picture of the circle symbol)

Lastly, we learned how to use CPCTC in a proof and that radii imply congruent segments. 

This was basically what we did, except it was obviously one circle, circle O. I couldn't figure out a good way to make the proof (sorry), but we proved that seg. AB was congruent to seg. CD, with CPCTC reason they were congruent. 

That's pretty much what we did in class today!

-Jessica 

Section 3.2 : Three ways to prove triangles congruent

Today we learned how to prove congruent triangles using postulates and theorems. We proves the postulates and theorems using a triangle construction worksheet. You know the postulate or theorem works when there is only one true possible way to make the triangle complete. (sorry it's blurry, but this is the worksheet we did during class)

I put check marks next to the postulates/theorems that worked, and an x by the one that did not. S means Side, and A means angle.
Postulates/theorems that will work:
SSS
SAS
ASA
AAS
Postulates/theorems that will NOT work:
SSA
AAA

*Working postulates/theorems may be used in a proof as a justification to prove justification, and you only have to right the side-angle combination. (i.e. SAS, SSS,...ect.)

Triangles may also be similar, meaning there angles are congruent but sides are not. (Hence the reason AAA does not work)

Well I'm pretty sure that's about all we covered :D
Yupp!
Have fun with the homework, sorry this is so late!
-Maggie Ridenour

Chapter 2 Review

I created a wiki for our review sheet.

Every problem is on a different page.  You can upload an idea, the beginning of a solution, or a whole solution.  You can also edit anybody else's response to improve it.

Here's our wiki:
http://hga1f10.wikispaces.com/

If you've never used a wiki, check out this video.
http://www.youtube.com/watch?v=-dnL00TdmLY